The Theory of Parallel Lines, Being an Attempt to Demonstrate the Twelfth Axiom of Euclid.

 

By Daniel Wilkie

 

[Originally published by the Literary and Historical Society of Quebec in Transactions, Original Series, Volume 3 (1837)]

 

READ BEFORE THE SOCIETY ON THE 21ST JAN., 1832.

 

In the following paper, the truth of the first eleven axioms, and of the first twenty-six propositions of the first book of Euclid, and of these only, is to be admitted.

 

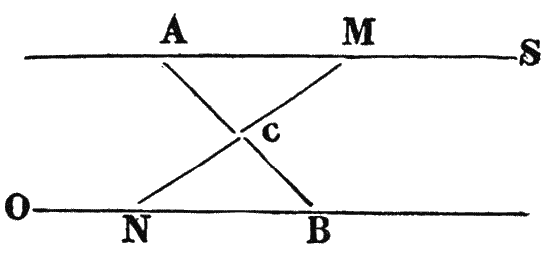
DEFINITIONS. — I. When a line cuts two other lines, the angles on the opposite sides of the cutting line, and at its opposite extremities, are called ALTERNATE angles.

 

II. When a line cuts two other lines, making the alternate angles equal, these two lines are said to be PARALLEL.

 

 

Thus, if the line HI cut the two lines AB, DE, the angles ACF and CFE are called alternate; and also BCF and CFD.

 

THEOREM 1. — If a line cut two other lines, making one pair of the alternate angles equal, the remaining pair shall also be equal.

 

Thus, if the angle ACF be equal to CFE, the remaining pair of alternate angles, BCF and CFD, shall also be equal.

 

For, the angles ACF, BCF, being equal to two right angles (XIII. 1. Eucl.), and CFD, CFE, being also equal to two right angles; the two ACF, BCF, are equal to CFD, CFE (Ax. 1.). And since ACF is equal to CFE, the remainder BCF is equal to the remainder CFD. — Q. E. D.

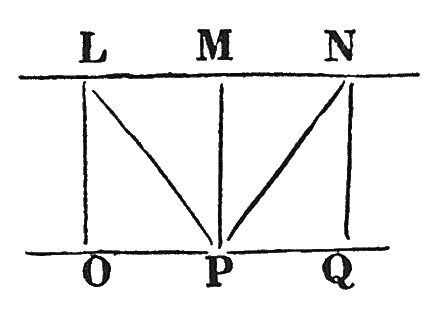
THEOREM. 2. — If a line cut two parallel lines, any line bisecting the line which cuts them will have its alternate angles

 

Let AM be parallel to NB, in consequence of the line AB cutting them, and having its alternate angles equal; any line, as NM, bisecting AB in C, and meeting the parallel lines, shall have its alternate angles also equal.

 

For, the angle MAC being equal to CBN by supposition, and the opposite angles ACM, BCN also equal (XV. 1. Eucl.) and likewise the side AC equal to CB by construction, the two triangles are entirely equal (XXVI. 1. Eucl.). Hence, the angle AMC is equal to the angle CNB, and they are alternate angles. Hence, also, the angle MNO is equal to NMS. Wherefore, any line bisecting AB, and meeting the parallel lines, makes its alternate angles equal, as was to be shown.

 

COR. — Hence, a line passing through the point C, and perpendicular to the one line, is perpendicular to both[1].

 

THEOREM 3. — The perpendiculars to one of two parallel lines, drawn from points in the other, which are at equal distances from the line which is perpendicular to both, are equal to one another.

 

Let AC and DE be parallel, and let BE be the line which (by Cor. Prop. 2.) is perpendicular to both; and let the points A and C, be at equal distances from B, the perpendiculars let fall from these points upon the other parallel, are equal to one another.

For, if AE and EC be drawn, the triangles ABE, CBE having AB equal to CB by supposition, BE common, and the angle ABE equal CBE being both right angles; are entirely equal. (Eucl. I. 4.) Consequently the line AE equal to CE the angle BEA equal to BEC.

 

Also, let AD be perpendicular to DF, and having made EF equal to ED, join CF. Then, the whole angle BEF being equal to the whole BED, and the part BEC equal to the part BEA, the remainder CEF is equal to the remainder AED.

 

Hence, the triangles AED, CEF having the two sides and the angle between them in the one, equal to the two sides and the angle between them in the other, are entirely equal, (by IV. of the first.) 1'herefore the angle at F is equal to the angle at D, which is a right angle, and CF equal to AD.

 

Wherefore AD and CF, which are perpendicular to DF, and drawn from the points A and C at equal distances from the point B, are equal to one another. — Q. E. D.

 

THEOREM 4. — If a line cut two lines, making the alternate angles unequal, every line bisecting that line, and meeting the other two, shall make unequal angles with these two.

 

Thus, if the line AF cut the two lines AI, HF, making the alternate angles AFH, FAI, unequal, every line bisecting AF, and meeting AI, and HF shall have its alternate angles unequal.

 

For, since the angle FAI is unequal to AFE, let FAB be equal to AFE, that is let AB be parellel to HF, then, let AF be bisected in C, and through it, draw ECB, cutting the two parallels in B and E: the angle ABC is equal to CEF (by the 2d of this paper.) But the angle CDA is greater than the interior opposite one CBA, (Eucl. I. 16.) and consequently greater than CEF. That is, the alternate angles are unequal. In the same manner, any line bisecting AF and meeting the lines AI and HF may be shown to have its alternate angles unequal. — Q. E. D.

 

COR. — Hence it is manifest that the line bisecting AF and drawn perpendicular to HF, will make unequal angles with AI. That is,

 

If a line cut two lines, making the alternate angles unequal, the line which bisects that line and is perpendicular to one of the two lines, makes oblique angles with  the other.

 

THEOREM. 5. — If a line cut two other lines, making the alternate angles unequal, the lines drawn from the one line perpendicular to the other, will continually decrease, the nearer to the acute angle being always greater than the more remote: on the other hand, these perpendiculars will continually increase on the side of the obtuse angle, the nearer being always less than the one more remote.

 

Thus, if BF cut the two lines AC, DE, and make unequal angles with them, so that BFD may be a right angle, while FBC is acute (by the 4th of this paper,) then, if from any other points L and K in the line AC, perpendiculars be let fall upon DE at M and I, LM shall be less than BF, and KI less than LM. Also, BF is less than GH, and GH less than any perpendicular beyond it.

 

For, supposing FK to be perpendicular to AC, then, in the triangle FBK, right angled at K, the side BF is greater than FK (Eucl. I. 19.) For the same reason, in the triangle FKI, right-angled at I, the side FK is greater than KI. Much more, then, BF which was proved to be greater than FK, is greater than KI.

 

Further, let L be any point between B and K, then, upon drawing LM perpendicular to DE, the triangle BFL must have the angle BLF obtuse because greater (by Eucl. I. 16.) than the inward opposite angle FKL which is right. Therefore, in the triangle BFL, the side BF, opposite to the obtuse angle BLF, is greater than the side FL opposite to the acute angle FBL, (Eucl. I. 19.) For the same reason, in the triangle FLM, the side FL opposite the right-angled FML, is greater than LM, opposite to the acute angle LFM, which is acute because only a part of the right-angle BFM. Much more must the line BF, which was proved to be greater than FL, be greater than LM. For the like reasons, LM is greater than MK, and MK greater than KI. Much more, then, is LM greater than KI.

 

Thus, it appears, that perpendiculars to DE, drawn from points in the line AC, continually decrease as these points recede from the acute angle at B. And in the same manner, it may be proved that perpendiculars to DE, drawn from points in the AC, continually increase as these points recede from the obtuse angle at B, as asserted.[2]

 

THEOREM 6. — Every line which is perpendicular to one of two parallel lines, is perpendicular to the other.

 

Let the lines AC, DF be parallel, having BE perpendicular to both (by the Cor. to our 2d;) any other line perpendicular to the one shall be perpendicular to the other.

 

For, if BA be taken equal to BC, and AD, CF be both drawn perpendicular to DF, these perpendiculars shall be equal (by the 3d of this paper.) But of CF had its alternate angles unequal, no other perpendicular as AD, drawn from AC to DF, could be equal to CF. Therefore since AD is equal to CF, the angle BCF is equal to CFH, which is a right angle. Hence, FC is perpendicular to AC. And, in the same manner, any other perpendicular to DF may be shown to be so to AC.

 

THEOREM 7. — Parallel lines are every where at the same perpendicular distance.

 

Let LM and OQ be parallel, or have the alternate angles formed by some line cutting these equal, any perpendiculars to them, as LO, NQ shall be equal.

 

For, bisect LN in M (Eucl. I. 10.) and join LP and PN. Also, let PM be perpendicular to LM, and it will be so to OQ, (6.) Then, the triangles LMP, MNP are entirely equal, (Eucl. I. 4.) and have the side LP equal to NP and the angles PLM, LPM, respectively equal to MNP, MPN. Now since the whole MLO is equal to MNQ (6.) and the part MLP equal to MNP, the remainder OLP is equal to the remainder QNP. In like manner the angle LPO is equal to the angle NPQ. Wherefore the triangles OLP and QNP, having two angles equal, and the side LP equal to PN (Eucl. I. 26.) are entirely equal. Hence the side LO is equal to the side NQ, and thus all the perpendiculars cutting the two lines, may be shown to be equal.

 

THEOREM 8. — If a line cut two other lines, making the alternate angles unequal, the two lines will meet, if produced, on the side of the acute angle.

 

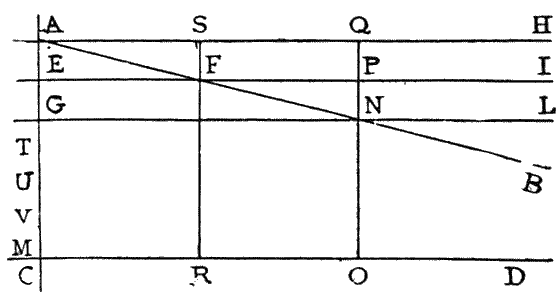
Let AC cut the two lines AB, CD, making the alternate angles unequal to each other, the lines AB, CD will meet, if produced, on the sides on which one angle is acute, or less than the adjacent. For example, let AC be perpendicular to CD, and have the angle CAB, alternate to ACM, acute, AB and CD will meet, if produced, towards B and D.

 

To prove this, take AF, FN, equal distances on the lines AB, and through the point F, draw EFP parallel to CD; then EP is perpendicular to AC, (6.) and the angles AEF and FEC are right angles. Through A and N, draw AH and LNG, both parallel to CD. Then, draw NQ parallel to AC, that is (Def. 2.) make the angle ANQ equal to the angle FAE (Eucl. I. 23.)

Hence, the triangles FAE, FNP, having the angle NFP equal to the angle AFE, (Eucl. I. 15.) and the angle FAE equal to the alternate angle FNP, (by Hyp.) also the side AF equal to the FN, (also by Hyp.) are entirely equal (Eucl. I. 26.) Wherefore the side AE is equal to the side PN.

 

But the lines PN and EG being perpendicular to the two parallel lines GL and EI, are equal, (7.) Hence GE is equal to EA, and EA is also equal to FS, (7.) also, RF is equal to CE, and ON equal to CG, (7.)

 

In thus manifestly appears, that AC, FR, NO, the perpendiculars let fall from AB upon CD, at the equisistant points, A, F, N, decrease by the equal differences, AE, EG. In the same manner, if more points be taken on AB, at distances each equal to AF, the perpendiculars let fall from these points upon CD, will decrease by differences each equal to AE. — By taking AE, therefore, a sufficient number of times, it must at last, either end at C, or beyond it at X. But, by taking AF the same number of times upon AB, it must at last end in the line CD, or on the other side, since it has been just shown, that every line joining the corresponding points in AC, and AB, is perpendicular to AC, and therefore parallel to CD. If, for example, four times AE should be found equal to AC, four times AF must end precisely in some point of the line CD, (Eucl. I. 11. Cor.); but if AC should be found to be more than four times, but less than five times AE, then, four times AF would not meet CD produced, but five times would pass it. Hence AB and CD, being both produced, must meet, and it is on the side of the acute angle, that they meet.

 

QUEBEC, December 27th, 1831.

 

In the preceding paper, I have endeavored to remove the defect under which the science of Geometry has hitherto laboured from the imperfect elucidation of parallel lines. To this attempt I alluded in my paper on "Space and Length," inserted in the second volume of the transactions of this Society.

 

I have not had the pleasure of seeing the methods proposed by Legendre to remedy this defect. According to Professor Playfair, one of his methods is founded on the abstract doctrine of Functions, and therefore unsuitable to be proposed to such as are entering on the study of Geometry. The other method is also stated by the same Professor to be of too abstruse, extensive and intricate a nature to form part of an elementary system of that science. An ingenious demonstration of this property of Parallel lines. was published in the Philosophical Magazine for 1822, by Mr. Ivory; but it is also very complicated. As far as I can judge, the preceding Theory is sufficiently simple to be put into the hands of the youngest students of Geometry. The 5th proposition and the last might be rendered more easy of comprehension by dividing each of them into two, a distribution of which they will readily admit.

 

In communicating this Theory I beg further to state, that it forms part of a system of Geometry which occupied my leisure hours for several years, and which is now nearly completed. Of that system, the fragment now presented, may be considered as a fair specimen, except as far as it was necessary to omit all reference to the larger work, in an extract requiring to be read independently by the lovers of demonstrative science. The extract has only been so far altered as to render it susceptible of separate perusal.

 

This system of Geometry, on which I have bestowed a good deal of attention, possesses the following peculiarities, which, of course, I consider as so many advantages.

 

1. The usual treatises on this subject, presuppose the use of the ruler and compass. That which I speak of, presupposes only the use of the ruler. The properties and use of the compass are in it derived from first principles, by the same synthetical reasoning, upon which the whole science depends.

 

2. The definitions, on which it is well known that this science is entirely built, are all strictly logical. The terms which cannot be logically defined, are explained, and the principles they involve, assumed on their proper grounds.

 

3. No definition is attempted, till the property which it involves is shown to be possible, or assumed to be so.

 

4. All the propositions are simple. It is at no time attempted to prove two or more properties of a geometrical figure in the same demonstration. But where a series of truths are intimately connected so as to require a connected view to be given of them, such a view is given of them in scholia or notes appended to the propositions.

 

There are other minor points of difference which need not be here enumerated. The object has been, to combine the strictest geometrical reasoning with the most lucid illustration of which the subject admits. Particular care has been taken to render the introductory demonstrations as simple and easy as possible. When a habit of geometrical reasoning has once been formed, greater consciseness of expression, and more difficult forms of ratiocination, may be safely admitted.