An Elementary Discussion of the Nebular Hypothesis

 

By William Austin Ashe

 

[Published by the Literary and Historical Society of Quebec in Transactions, New Series, No. 19 (1889)]

 

There may have been a time when a lecturer on such a subject as I propose to bring before you this evening, felt apologetically inclined towards the lady portion of his audience. To-day, in the days of Girls' High Schools, with its increasing tendency to Universology, and the advantages which are very evidently taken of the increased opportunity, makes one also feel apologetically inclined towards an audience, but upon entirely different grounds. Why, it was but the other day that I took pity on one of your sex, who I thought might form one of my audience here to-night, and was explaining to her the fundamental principles of my subject, so that she might be in a position to grasp the conclusions which are to follow. Then I learnt, that, not only have we institutions here which teach, but that they teach in such a manner that the teaching is remembered, even when woman has settled down into that sphere which is so essentially and becomingly hers.

 

I propose explaining to you this evening, in a very elementary way, such of the general principles of the Nebular Hypothesis as will permit of this treatment ; I cannot therefore promise a complete demonstration, even if such were possible, as to do so would require more time than we have at our disposal, and a higher degree of mathematical reasoning and analysis, than it is likely you would be prepared for, or I, myself, prepared to give ; but, at the same time, although we may thus be debarred from the full understanding of the subtle reasoning and treatment that this subject generally receives, I conceive we shall have no difficulty in attaining somewhat the same ends, in the manner I have proposed to myself. To those of you, who are more advanced than the methods I shall make use of, I have no apology to offer ; this is be an elementary discussion, and I presume you are here to hear it,—besides, my experience has invariably been that there is something to be learnt from even the most mediocral treatment of a subject at the hands of a tyro ; for although there may be no new facts presented, or valuable conclusions drawn, there is always the benefit to be had, in the view of a subject from another's standpoint, which, I take it, will always present points of interest to the student. And, whilst I hope that this is not the only grounds on which my occupying your time this evening will be excusable, I mention it here as a justification for the primitive way in which my subject will be treated, to those for whom the method will be otherwise unprofitable.

 

The evidence of the correctness of a theory or hypothesis, increases with the number of facts it is capable of satisfactorily explaining. It diminishes with the number of facts it does not explain, and with the number of different ways in which similar phenomena can be explained. A single fact, inconsistent with any theory or hypothesis, is sufficient to overthrow it ; and it is quite remarkable, how long the time is that is required to prove a fact sufficiently inconsistent to overthrow an established theory. “We all know how Gallileo, with his imperfect telescope, saw that the moon's surface was broken up into mountains and depressions ; and, how the accepted theory at the time persisted in its being a perfect sphere. Even when confronted, with the evidence of their own eyes, they made the somewhat incongruous statements, that although it looked an even surface, this unevenness was covered over by a smooth, perfectly transparent, and therefore invisible surface, which reduced it once again to the required outline. Gallileo, with a quaint, dry humour, cautioned them, that if they did not take care, he would drive them from their last remaining assumption, by insisting upon invisible mountains upon their invisible sphere.

 

It will be proper for me, before entering into my subject, to assure you that but few of the conclusions which we shall arrive at, are other than those which are generally accepted as parts of the hypothesis. Where it is otherwise, I shall protect your interests and my own by due notification. This may seem a somewhat idiosyncratical and egotistical announcement to make in connection with so well known, and eminently discussed hypothesis ; yet, because of the increase of the modern tendency to transcendental analysis, with which the greater minds occupy themselves in the contemplation of all questions ; and the constantly enlarging field, to which such analysis is pertinent, the muddy waters at the bottom of our living streams, are practically left to the occupancy of the smaller fry, whilst the leviathan disports himself in the higher regions, or makes excursions in search of other feeding grounds where his equally ambitious, less able confreres can not follow him. This allegory is intended to point out, how, although it may be unlikely, it is not impossible, that evidence of the special application of a fact to a theory or hypothesis is not entirely dependent on its environment.

 

I remember once having come across a very common everyday design and inscription. It was placed over the door of a house of entertainment, and to the ordinary passerby its meaning must have been very evident. It consisted of the orthodox “American Eagle”, holding a scroll in his beak ; on one side of this scroll was inscribed “RESTA” ; on the other, “URANT,” the two separated by about three feet as occupied by the intervening “eagle.” Happening to be passing by this house with a friend, who was a proficient classical scholar, I said to him ; “you are pretty well up in this sort of thing, what does it mean ?” And he answered, from out a mind forever suspicious of the presence of a classical root, and oblivious to the very evident signs indicative of the establishment being the dispensary of a root, which is quite freely described as basic to all evil ; that it was, “possibly an idiomatical expression, indifferently expressed, announcing the fact, that, 'The thing which remains, they are burnt,' but where the application of the saying was, he could not see.”

 

As we are about the discussion of an hypothesis, you will understand, that, it cannot be proved the assumed developments have taken place,— we must satisfy ourselves, for the present, with the assurance that these developments are possible, and probable, then patiently wait, 'till actual observation shews a change in some member of our system, or any other, in accordance with the tenets of our hypothesis, and in the required direction ; which we may then safely claim as the visible outcome of the hypothetical forces.

 

It will be instructive to us, to consider the reasons which pointed to the necessity for the adoption of some such belief as is contained in our hypothesis, so that the questions it proposes to solve, should not be considered as the result of chance, rather than uniformity of design.

 

First, the motions of the members of our system are perfectly uniform, in directions which are uncontrolled by the laws of gravity or attraction : for example, the 250 members of our system revolve about their common centre, the sun, in the same direction. Now, the probability of this uniformity of motion being the result of accident rather than some common cause, is represented by the proportion which the number 1, or unity, bears to a quantity having 60 figures in it, say, the number 5 and fifty-nine noughts, whatever this would represent when numerated ; we are therefore almost absolutely certain, that there was a common cause for this uniformity.

 

Then, all the planets move in orbits, or paths, which lie nearly in the same plane.

 

All the planets, that have secondaries, moons or satellites, have their movement about the planet, or primary, in the same direction, excepting that of the planet Uranus.

 

None of the paths or orbits of the planets are inclined to those of the Asteroids, or minor planets, more than an angle of 45°.

 

And finally, we cannot account for the undiminished heat-giving power of the sun, without some such hypothesis ; nor by any other such hypothesis in such a completely satisfactory way.

 

The heat given out by the sun has been estimated ; and of this amount, we, the earth, receive one millionth part ; the remaining members of the system each about a like amount. There thus remains, of the heat given out by our sun, an enormous quantity, which, as far as we know, is not intercepted and passes off into space, to be lost, it is assumed. Yet, the supply is not getting less, as far as it is possible to determine from the records of the past, extending over historical times, which point to climatic conditions being the same to-day as then. Yet, if we consider the sun, simply as a molten radiating body, giving out its heat in this way ; at its present rate of expenditure, we know that it must have cooled many thousand degrees within the time covered by this record. We must, therefore, conclude that this loss of heat in the sun is made good from some source ; and there is no more satisfactory way of so accounting for this compensation than in the manner proposed.

 

It is estimated that it would take twenty tons of coal a day, to each square-foot of. the sun's surface to supply the energy given out in the form of heat, in the same time. Even if the sun were a solid mass of coal in the first place, it would have been entirely consumed in a few thousand years. It is not possible to imagine, any combinations of the elements that the spectroscope shews as under combustion in the sun, which would be capable of maintaining such undiminished energy in this direction, for so lengthy a time as has evidently been the case. And finally, the only other theory, which has sufficient plausibility in its favor to permit of our considering it in this connection, is the assumption that the sun's heat is maintained by the heat developed from the impact of innumerable meteors, which are drawn to the surface of the sun from their orbits about it, by its attractive energy. This supposition does not receive very general support, because of the enormous mass of such matter which would be required, or the inconceivable velocities that a smaller number must attain, to maintain the required moment of combustion. There can be no doubt that this meteoric impact is a source of heat to the sun, but it is very generally conceded that it is merely an aid to the greater compensating powers contained in the principles of the hypothesis we are discussing.

 

We are all familiar with the fact, that, if the temperature of this or any room is, say, 60 ° and the walls are brought together, so that the space within it is reduced one half whilst the amount of atmosphere it contains remains the same, although in a more condensed arrangement, that the temperature will have been increased correspondingly. It was Sir William Herschel [the elder] who adapted this knowledge to the requirements of the sun and the Nebular hypothesis, shewing how an inappreciable contraction of its diameters would compensate for the heat given out ; and it has been estimated that a contraction in these measures, of four miles a century, would make up the heat radiated in this time. And, paradoxical as it may seem when viewed in the light of our experience of cooling and necessarily contracting bodies, it is possible that a body contracting because it is giving out it's heat, should in its contracted form be at a higher temperature than when in its first condition. This corollary is an essential part of the endeavor to account for the conservation of the solar heat-energy, for if we merely insist that the sun has lost heat and that the diameters have correspondingly contracted, although we have our sun with reduced dimensions it is inevitable that we can have ipso facto no increase of heat. Yet, this certainty of the decrease in the sun's diameters has an important bearing on the initial argument in the hypothesis ; for, if we admit that the sun is contracting its diameters at the rate of four miles a century, a century ago they were this much greater than to-day, two centuries ago eight miles greater, and, there being no definite limits which we may not set, for the period of time over which we assume ourselves as looking, we can conceive the possibility of the matter which forms the material of the sun, filling, if needs be, the whole of the present limits of his system ; particularly when we remember the additional fact, that the present rate of contraction, is certainly less than that which existed at the beginning ; so that, although it is assumed that the total period of existence for the sun, and necessarily therefore for the members themselves, as far as the possibility of their maintaining life as we now know it upon them, is concerned, is limited at about thirty millions of years, of which about fifteen millions have elapsed, this last period would suffice for the retrospective arguments just advanced, and enable us to accept, with some certainty, the fundamental assumption of this hypothesis ; which assumes, that all matter at present forming the members of the solar system, originally existed in space as one, almost uniform, nebulous mass ; from whence, through the different stages of planetary existence, the several members of our system have been evolved.

 

Sir William Herschel pointed out, how, the sun being only a star, and equal in size to a so-called tenth magnitude star, we see some nebulæ in the heavens which are perfectly uniform or nebulous in appearance, which would represent the first condition of our hypothesis ; others, with a bright nucleus or centre, which would represent what will later become the central or controlling body of the system, like our sun ; others, with additional well defined bright points, representing a further condition of development ; and, a final condition, in which we see several stars, the larger members of the system (distance preventing our seeing the smaller), performing their revolutions about the central mass, the nebulous part of the system having in the meantime been absorbed.

 

We have thus illustrations of the several conditions assumed in our hypothesis, but they are taken from systems simultaneously existing in these several conditions ; no one system showing them co-existent, because the process of change is so gradual and relatively contemporaneous, that each system must shew a condition rather than a series of conditions. Were there a system situated sufficiently near to us, it would be possible, in all probability, to distinguish small changes of condition ; the enormous distances that exist in fact, prevent our witnessing any other than the radical changes which take place in their developments; and centuries must elapse, before we can point to any one system and declare, that there certain changes have taken place, in accordance with the requirements of our hypothesis.

 

Professor Newcomb has said :—“At the present time we can only say that the nebular hypothesis is indicated by the general tendency of the laws of nature, that it has not been proved inconsistent with any fact, that it is almost a necessary consequence of the only theory by which we can account for the origin and conservation of the sun's heat, but that it rests on the assumption that this conservation is to be explained by the laws of nature as we now see them in operation. Should any one be sceptical as to the sufficiency of these laws to account for the present state of things, science can furnish no evidence strong enough to overthrow his doubts, until the sun shall be found growing smaller by actual measurement, or the nebulae be actually seen to condense into stars and nebulæ.”

 

It has been offered as an objection to the Nebular Hypothesis, that it is an atheistical doctrine ; but, it appears to me, that this objection is founded on the atheistical assumption, that the minor developments of the hypothesis are not parts of the benificent scheme of the Almighty ; rather let us conclude, that there is as much evidence of design, of the presence of an all-wise Entity in the assumptions made use of in our hypothesis, as there is in the knowledge we have of the developments that take place from the life germ to the vegetable or animal completion. Carlyle has said, and there are few who will contradict him :—“This I say and would wish all men to know and lay to heart, that he who sees nought but mechanism in the universe, has in the fatallest way missed the secret of the universe altogether.”

 

We may place our first cause as far back in time as we like, but, no matter what our theory, we cannot dispense with it altogether. “We may call this principle accident or design in original creation, but we shall have rather increased the difficulties of our position ; for we shall only have substituted sentient matter for a sentient Being, and the difficulties as to original creation will be insurmountable.

 

Buts why should we attribute to accident such nicety of adjustment and uniformity in law?

 

Is it accident that causes a law to operate in a certain direction to a certain point, where, to continue beyond would entail destruction, and there to reverse the law ?

 

Instance the simple operation of freezing water. As the temperature decreases, each particles density increases and it sinks to the bottom. Now, if this law continued uniformly to the freezing point, all ice would form at the bottom of our rivers and lakes, and year by year would accumulate, till the earth became largely ice covered and unhabitable. Instead of this, accident has so arranged the process, that the increase in a particle's density ceases at a certain lowering of its temperature, beyond which the reverse of the law begins and continues ; so that the coldest particles come to the surface under its influence, and permit of ice being formed there. Again, particles of matter mutually attract each other, till they are brought within a certain infinitely small distance of each other, when the law is reversed and they are repelled. In illustration ; a certain amount of attraction keeps the particles forming any mass together ; it is the same force that is known as “attraction,” only in this connection it is generally called “cohesion” ; take the particular and most exaggerated example of the substance known as India rubber ; you distend it and its recovery is immediate ; you compress it, and it returns to its normal condition, movements which cannot be accounted for under any other supposition than that this tendency acts in opposite directions under different conditions, and that whilst the mass is at rest the particles have no tendency one way or the other. “Were this power of recovery not present in all matter, after undergoing distension or compression, existence would not be possible. Take, in illustration, the case of our lakes and rivers and our atmosphere, which would become so concentrated because of the various services that are made of them, that eventually they would become no longer suited to their several purposes. I need not add further illustrations, as the most casual observer, if he care to do so, will find for himself the truth of this statement, that each class of matter is endowed with properties, or has acquired them at hap-hazard, which are peculiar to itself or class, and that the law governing each class is more suited to the conditions it is called upon to fill, than any we could propose. Often familiarity with phenomena prevents a proper appreciation of the same.

 

There are two first conditions assumed for our Nebular Hypothesis ; one advanced by the elder Herschel, in which the figure or outline of the original mass is assumed to be that of a sphere ; the other maintained by Laplace, in which this outline is assumed as being that of a disc. Herschel reasoned that the sphere was the natural arrangement that the particles of such a mass would conform to ; Laplace argued, that as all the planets which have been developed out of this mass, occupy the same plane with their orbits, very nearly, the outline of the devolping figure must have closely co-incided with this. Both assumed that the mass had a revolution about its centre of gravity, and the centre a motion through space ; for even if we do not admit an origin for these motions, it is much more difficult to imagine the existence of this matter in space, entirely without motion, than with it ; either inherent or imparted. Now these two motions have descended to us, in the first place in the visible fact that our sun is travelling through space, and carrying the members of his system with him ; in the second place, in the experience that all the members of this system have a motion about the central sun, in the same direction ; and, although the connection may not at once be apparent, each member has a motion about its own axis, as far as known, also in the same direction, excepting, as before, the planet Uranus. It has been argued that the motion of aggregation that took place amongst the particles of the original mass towards each centre about to develop into a planetary body, is in itself sufficient to account for the motion about their respective axis, and we shall see how perfectly this assumption can be demonstrated ; but the orbital motions are not so easily accounted for without assuming a first impulse given to the mass from without. We must conclude that a motion was given to the mass as a whole, to have caused our sun to be travelling through space with us about him ; and if this motion was imparted to the undeveloped mass, in any direction other than along a line passing through the centre of the mass, this impulse must have resulted in a motion about that centre ; depending for amount, on how far from the centre of gravity of the whole mass, the prolongation of the direction in which this force was administered, would have passed from that centre. We have thus the grounds on which it can be reasonably assumed that the original mass was progressing through space, whilst, at the same time it was rotating about its centre of gravity ; the last a conclusion, which is of vital importance to the whole theory and its developments.

 

Before proceeding further, I must ask those of you who may not be familar with the subject, to accept on faith, just two propositions. The first known as the “parallelogram of forces” ; a mechanical method, employed to determine the effect of two forces acting simultaneously on the same point in a mass. The other, and more difficult to prove, is, that if any body or planet is revolving in an orbit with a certain velocity, it only requires it should be increased a little less than a half in amount, to cause the planet to leave the centre controlling it, (in our case the sun), and fly off into space ; or, conversely, to decrease this velocity in the same proportion, to cause the planet to fall into the same centre. Now, by means of this two propositions, I think we may investigate some of the most important developments that are supposed to hare taken place in our system, developing individual uniformity from the general mass.

 

We shall continually have to refer to two properties of matter ; one called the “centrifugal force”, the other the attraction of gravity, with both of which you all must be familiar.

 

Let us represent the first condition of our nebulous mass, as a ball or sphere in space, by a circle. It is manifestly impossible that this mass should be of uniform density throughout, as in nature elsewhere we know of no absolute uniformity strictly speaking. It is permissable then, for us to assume, that there are in our mass, centres of differing, therefore of greater, density, which we will further assume are distributed about the mass without any reference to systematic arrangement. Let us assume that the whole mass is turning about the vertical line A-J, and that our centres of greater density are situated indifferently at the points A, F, G, H, &c. In consequence of this rotation these centres will describe paths which we may represent by lines drawn through the several positions, at right-angles to the line A-J. Now as we have assumed any position for our centres of greater density, A, F, G, H, &c., and observation shews us that the planets which these centres have developed into by aggregation of the particles in their own neighborhood to themselves, occupy a relatively limited zone, it will be necessary to attempt the shewing of how this may have been brought about. Let us imagine ourselves as looking down on the orbits which these centres are describing about the centre of the mass, from the direction of the prolongation of the line A-J ; then the line A-J will be represented by the central point A, and the paths of the several incipient planets, by concentric circles. Now, the laws governing the centrifugal force inform us, that similar bodies revolving in unequal circles in the same time, induce centrifugal forces corresponding to the radii of the several circles described ; so that “A”, representing the position of the centre of the circles we have drawn, the distances from the centre A, to each of these, will represent the amount of the centrifugal force in each case ; from which it will be seen that the point A, having no such tendency, being on the axis A-J, will under the action of gravity alone, fall along the line A-J to the centre of the system. “We have thus one position where, had a centre of aggregation existed and developed into a planet, it must have fallen towards the centre, and have been absorbed by the central mass, being unable to establish an orbit about it. Let us see what other positions would have resulted in this way, and where the limits would occur, between those planets which when developed could maintain an orbit, and those which could not.

 

Let us first consider the case of a centre of aggregation which is assumed as situate at the equator of our rotating nebulous mass. If the amount of rotation that the mass has obtained is sufficiently great to have developed a centrifugal force at our incipient planet's position, greater than the attraction of gravity, the nebulous mass will throw off into space all those particles which are so influenced, and with them our assumed centre of aggregation. We must therefore assumed that the motion of rotation of our nebulous mass has such a value, that at the equator gravity equals the centrifugal force or is less than it, or that being greater the particles thrown off reduce it to this condition. Gravity being equal to the centrifugal force, the orbit developed by our planet will be circular, and there will be a constant tendency to leave the centre of the mass which will be always equalled by the tendency which draws it towards centre of the same. We have thus determined the positions in which a developed planet would have no tendency to leave the centre of the mass, falling directly towards it ; and the position where both these tendencies are equal. It might be argued from this, that at an intermediate position if a planet where being developed, it would have tendencies intermediate between these two ; or, that it would describe an orbit which would enable it to pass so as to touch the central mass ; and we shall find this to be true from the proposition already established, which requires that the velocity of a body in an orbit, such as is being described by our assumed equatorial planet, should be increased only a half to cause it to leave the controlling body, with its converse ; and a consideration of the diagram which we have drawn shewing these orbits passing through the positions of our assumed planets as concentrict circles, will shew us, that as all our planets performed their orbits in the first place as portions of the same original mass, in the same times, that we may consider the lengths of these several circles as representing the respective velocities in the same, which are again proportional to the raddii of the several circles and vary as the cosine of the angular distance of their positions from the equator of the mass. So that if we assume the radius to the orbit in the declination 45°, as being equal to unity, that at the equator of the mass will be equal to 1.414, the increase necessary to cause a planet acquiring it to travel off into space ; and conversely, if we consider the equatorial velocity as being equal to unity, the velocity at 45° will be 0.849 or that with which it would be impossible to maintain an orbit. We may thus conclude, that planetary aggregation may have taken place, and indeed must have taken place, indifferently with regard to position in the first place, but that all developments which took place more towards the poles of the mass than 45° must have been unable to continue existence as independent members of the system, becoming absorbed by the central mass ; and we may thus bring Herschells assumption into agrement with the present visible outcome ; in which, as already stated, none of the orbits of the members of our system are more inclined than 45° to the equator of the same. In the first place our undeveloped but developing planets were revolving as an integral part of the whole mass, and in consequence were revolving in an orbit which has as its centre a point in the axis to the whole mass opposite to their position ; distant, from the centre of the mass by an amount equal to the sine of its declination, or angular distance from the plane of the equator. To day, all the members of our system have orbits about the centre of the system, or sun ; and, it will be evident that this change in the direction of the controlling tendency, must have produced effects, which it may be of interest to us to try and trace from this source. By means of our parallogram of forces, the position we assume for that of our developing planet, and the respective values of the actions of gravity and the contrifugal force, we shall find that the resulting tendency has been a force which will ultimately bring our planet very nearly into the plane of the equator of the mass ; but it will have brought with it into this position, certain characteristics, which, although they may not have been entirely unaltered during the progress of the body into its final position, yet will be sufficiently so to enable us with certainty to say, whether the present position of the planet, is that of its development or not. The forces that were effective in transferring our aggregation towards the equator, being small, occupied a very long time in their object ; we are therefore very certain that each planetary centre had practically completed aggregation before attaining their final position about the plane of the equator of the mass ; we cannot assume any one position, therefore, in which this aggregation could be assumed as being entirely performed in, but we may assume a mean position, in which we may infer all the developments of the planet from the mass to have taken place. In this mean position our planet will have acquired a characteristic motion about its axis, (the present diurnal-motion,) which, from the fact of aggregation having taken place equally from every direction, within sensible limits, will have been established at right angles to the line joining the mean-position with the centre of the system or mass ; and, as there has been no force effective to disturb the direction of this axis on the planet's way towards the plane of the equator of the mass, it should have reached its final position with this characteristic intact. The converse of the argument should enable us, by means of the present inclination of the axis of the planets with reference to the plane of the ecliptic, (the former equator of the original mass), to determine the position of the origin of the planet ; for there are but two positions in the meridians of the original mass' sphere, where this diurnal axis will be tangent to it and so determine the position where it originated,—one in either hemisphere, in opposite latitudes or declinations ; and it is important to remember that the conclusion deduced, to the effect that no developing planet could have maintained an orbit in a greater declination than that of 45°, is fully borne out by the conclusion here drawn as to the positions that may be deduced as above for the conception of a planet.

 

We shall now attempt an explanation of the action of the forces which have given each member of our system their diurnal motion, or that motion which produced the effect of “day” and “night”.

 

Let us draw a straight line and mark its middle point “A”, to represent the position occupied by a centre of aggregation ; one extremity, “C”, to mark the centre of the nebulous mass about which the whole of its particles, and with it of course our point “A”, are revolving ; and the other extremity “B”, which we will assume as equally distant with “C” from the point “A”. Now, if we further assume that the limits from which the centre “A”, can attract to itself particles of matter, is, in the one direction “C”, it will be sufficient for our purpose to assume that the opposite limit is “B”. A particle at “C” will have been at rest, as it is at the centre of the system ; so that on being drawn towards “A”, which is travelling about “C” with the motion of the whole mass, it will act as a retarding influence on that side of it which is towards the centre “C” ; whereas, a particle coming from “B”, having had there a velocity as a portion of the whole mass, greater than that belonging to the position occupied by “A”, it will reach the surface of our incipient planet, and act as an acceleration to it on that side which is towards the direction from which it came. It will be very evident then, that, the result of this acceleration on one side, and retardation on the other of our developing planet, will be a motion of rotation about its own centre in a direction corresponding to that which the mass had as a whole ; and this is precisely what we observe as the uniform relation between the diurnal-motions of the several members of our system, and their orbital motions.

 

It should have been evident to us, whilst considering how this diurnal-motion has been developed by aggregation from every direction, that as each particle of matter so added to the developing mass has produced a retardation or acceleration, in accordance with whether it has come from towards the centre of the system or from beyond the position of the incipient planet, each particle has tended to produce its consequent diurnal-motion about an axis at right-angles to the direction of its approach ; and as the approach of particles and their assimilation by the developing planet, has necessarily been assumed as being from every direction, there will have been an equal number in opposite directions, (that is, making the same angle with the plane passing through the centres of the system and the planet, but on opposite sides of it), to counteract the tendency that each has produced to alteration in the direction of the axis of the diurnal-motion to a motion at right-angles to its approach ; so that the diurnal-motion will be developed about an axis at right-angles to the plane passing through the centres of the planet and system, as previously mentioned. I have thus shewn the origin of the diurnal-motions from the manner in which they have aggregated to themselves the particles of matter from the original mass which form the present components of their several masses ; but, this aggregation has produced, or converted another motion as well. Let us again consider the case of two particles of matter reaching the developing planet “A”, from opposite and equal distances “C”, towards the centre of the original mass, and “B” from beyond the planet. If there were no other forces at work, further than the attraction of the planetary centre “A”, these particles would reach it with equal velocities, having travelled over equal distances in equal times ; but, instead of this being the case, we have the centre of the original mass, to which in the first place every particle forming it has a tendency, modifying the motions of approach of the particles “B” and “C”, towards “A”, so that that which approaches from “B” has its motion accelerated over and above the amount depending on the attraction of the planetary centre, by the amount attributable to the influence of the centre of the original mass ; whilst, on the other hand, that approaching from “C”, towards the centre of the mass, has it motion retarded by the amount attributable to the same influence. The result of this difference in the motions, or the impacts which each particle delivers to our developing centre, will have been equivalent to a thrust, or more properly speaking a series of thrusts, on our planet towards the centre of the mass, equal in amount to the difference between the final velocities with which these particles reach the surface of the planet. The immediate outcome of this must have been, first that our planet was brought nearer to the centre of the system ; next, that the planetary orbit, even if it were a circular one in the first place, must then have become an elliptical one, or, if elliptical, more elliptical. Could we assume that this difference in the velocity of aggregation took place as a single effort administered at a single point, or could we assume a mean position for the administration, we should be able to determine the point of the several planets' orbits which would be furthest away from the centre of the system or the “aphelion”. From the nature of the case, not being able to do so, we may yet be able to draw certain other conclusions from this effect, which I think will be interesting, at least. If we have a force which, whilst our planet is revolving about the centre of the system, is constantly altering the position of the aphelion in the direction of the planets motion, we should have an effect which should be operative continously in the same direction after the cause had ceased ; or, in other words, we should have a reason why the longitude of the aphelion should be increasing. And just in the same way, or for the same reasons that when we liberate a pendulum it does not come to rest at the lowest point of its arc ; so the extreme distances of a planet from the centre of the system, should not be a fixed quantity, but be subject to cyclical variation, altho' we will have to admit that this alteration in the distance of the aphelion, and values dependent upon it, will be a relatively small quantity, and in most cases, impossible to determine on this account. Then, whilst this difference in the velocities with which our particles are being aggregated, was present in the case of each planetary development, the position of any such centre, with reference to the centre of the system, will have very largely influenced the effect, in this way ; supposing two centres of aggregation, one situated relatively near to the centre of the system, the other correspondingly far from it, and both controlling equal areas by their attractions ; then, gravity proceeding from the mass as a whole varying inversely as the square of the distance, the difference between the effects of the particles arriving at our two centres, will be sensibly greater in the first than in the last case we have supposed ; and, as this difference in the velocities of approach of these particles, is assumed as being a factor in determining the ellipticity of the orbits of the several planets, the truth of the assumption will be evident from the fact that the ellipticities of the planetary orbits decrease with their distance from the centre of the system, with sufficient uniformity to permit of our accepting the general truth of our theory. The varying eccentricities and ellipticities of the planetary orbits, are not entirely deducible from this cause ; it is advanced as a cause, and an important one. If we assume, that the system of Uranus, for instance, was developing whilst revolving about the central sun, in a circular orbit; then, the systems, situate nearer the centre of the system, must have been revolving with velocities much less than that required to maintain themselves in circular orbits, and the amount of this deficiency being greater in proportion to the nearness of the planetary centre to the centre of the system, the larger the amount of ellipiticity necessary to the stability of the orbit ; for, it is evident that, the greater the deficiency between the velocity necessary to the maintainence of a circular orbit and the velocity which our planet has, the closer will it pass to the sun and the greater the difference between its final orbit and a circular one. Many of you are probably familiar with the law which connects the distances of the planets from the sun, with the times in which they complete their orbits about the same. This is a law that is invariable, shewing' small departures from absolute agreement in every case, but of such insignificance, relatively, as to make universal acceptance of this law deduced, not deductively but intuitively, by Kepler, acceptable ; not as being the law, but as representing it so nearly as to be equally efficient for all purposes, as the real law could be. I do not propose, as I hope you can imagine, attempting a reason where Kepler found none ; it is sufficient that I should draw your attention to the difficulty contained in the assumption that all the members were revolving about the centre of our system, in the same time ; and that at present, they revolve in times which though evidently deducible from their mean-distances from that centre, seem to have no connection with it. We might assume that the necessary parts of the original nebulous mass, had the required rates of revolution, and so get out of a difficulty by substituting another, to my mind, of greater difficulties. The difficulties in the way of satisfactorily connecting uniformity of motion in the original mass, with the orbital motions of the present members of our system are very present, but that does not necessarily imply that they cannot be satisfactorily overcome, as investigation proceeds. We see a reason why the time in which a planet performs its revolution about the centre of attraction, should lessen if its orbit becomes more elliptical, just in the same way that it is evident that if the orbit more nearly approaches a circular one, the period increases. Let me explain this further :—A relatively uniform nebulous mass can exist without disintegration, provided the effect of the motion of its rotation is not greater on any one particle of its matter than the inclination of the same towards the centre of the mass ; if it is less, there will be concentration towards the centre, limited by a disinclination amongst the particles themselves to closer arrangement than is normal to their condition ; but once aggregation takes place about the several denser centres, the material affording support in the direction of the centre of the mass, having been withdrawn, what was perforce a circular orbit, is either entirely destroyed by ending in the sun or centre of the system, or approaches much nearer to it, in the form of an elliptical orbit, than when in its circular condition. In one case its motion will have been constantly at right-angles to the action of gravity, in the other it will be more or less inclined towards it ; in the extreme case, in which we suppose it as passing just clear of the sun, it will perform one quarter of its orbit, in very nearly the same time that a body would fall to the centre from the same point, a period very much less than that required for it to complete the same proportion of its orbit at the uniform rate with which our imaginary particle started towards the centre, with a velocity increasing according to the laws of falling bodies, and along a sensibly shorter course (nearly the radius) than the quadrant ; the remaining three parts of both orbits will be performed under the same conditions, within limits that it is not necessary for us to follow here, so that we can readily understand, why a conversion of an orbit from a circular into an elliptical one, shortens the period, and the converse.

 

They who are un-familiar with the subject, generally have no difficulty in understanding how the first half of an elliptical orbit is described, under the influences of gravity and the centrifugal-force ; a difficulty is generally presented, to the understanding, when a diagram shews a planet as having reached that part of its orbit where the tendency towards the centre is greatest, on account of the planet having approached to its nearest in this direction, and then, under a diminishing centrifugal-force, as able to withdraw itself from destruction, and complete the rest of its orbit in the reverse order of the first part. As usually demonstrated, the evident fact would be an impossibility, for it will be readily seen, that, if a planet revolving in a particular part of its orbit, in response to the full effects of the forces acting at the instant, has arrived at a position, where the increase in the action of gravity is equalled by the centrifugal-force occasioned by the augmentation in the velocity that has resulted; our planet must continue to revolve, under such a supposition, in a circular orbit. The full explanation of the difficulty lies in the fact that, owing to the inertia of the planetary mass, the velocity corresponding to the influences of these two forces, cannot be developed till some time after the point where they were administered is passed. It thus happens that our planet's position and movements are always less advanced than the forces which are acting upon it in the first part of its orbit from aphelion, and less advanced in the remaining half. It thus happens that, at perihelion, although a maximum force has been administered the maximum velocity is not developed in the orbit till some distance beyond ; how little this may be, or how much, it is not necessary to determine ; it is sufficient for us to the full understanding of the question, to know that perihelion passed there will be a velocity developed, which will be greater than that corresponding to the planet's position, and that, on this account, it will be enable to withdraw itself, temporarily, from the super-control of the central system.

 

Many of the members of our system have secondaries, moons or satellites, accompanying them in their orbits ; these, with the exception of the satellite of Uranus, revolve about their primaries in the same direction as these primary planets do about the central sun, and on their axes. It is assumed that these secondary centres could not have formed by independent aggregation, in such close proximity to the larger attraction of their primaries. It is concluded, therefore, that they must have formed part of the planetary mass before radiation and consequent contraction reduced these bodies into their present solid forms, and that in this act of contracting they were left behind as a “ring” or rings, such as is visible about Saturn today ; and that further contraction of these rings resulted in their being rent asunder, whereupon the particles of matter re-arranged themselves about a common centre or centres, would thus become one or more satellites. There are one or two points about this part of our hypothesis, which do not appear to me to be fully accounted for : first, if contraction is taking place, because of the mass radiating its heat into space, the surface of our mass should be at a lower temperature than its centre, (the opposite conclusion, I am aware, has been advanced by a French writer, but does not seem to have been seriously entertained by those capable of forming an opinion,) and as such, should be in a more contracted condition than the surface beneath it, so that how, exactly, it is going to be left behind, by a smaller amount of contraction of the particles beneath it, seems to me an insurmountable difficulty. Then, contraction being equal along every diameter of our supposed planet, or, if we must supposed a difference, contraction being greater at its polar regions, and this the assumed cause of our “rings” being left behind, either a complete shell or envelope should be given off, or under unequal contraction, this ring should be given off from the position of greatest contraction, the poles ; and, in consequence, we might expect greater want of uniformity in the planes of each satellite's orbits, than we find to be the case, although, it is certain that eventually they would be brought into very nearly the same plane as the planet's equator. Again, this contraction having been a feature common to all the members of our system, why should not each and every member of the system have satellites, and why should there not be satellite's satellites, and so on?

 

As far as it has been possible to observe the fact, a satellite in revolving about its primary turns once on its own axis. This is very readily seen in the case of our satellite the moon ; for it is by means of this motion that she invariably keeps the same side towards us at all times. The same fact has been observed in the case of the larger satellites of Jupiter and Saturn ; it has therefore been concluded, perhaps hastily, that all satellites are in agreement in this respect.

 

If we assume all satellites to have been thrown off or left behind by their primaries, it should not be difficult to prove that they must have had periods of rotation on their axes and about their primaries, which were in close agreement in the first place, and later were reduced to exact agreement. It would be nearly as certain as a corollary, to state that, if a satellite revolves about its primary with a period differing largely from the time occupied in rotating about its own axis, this satellite cannot have been thrown off by the primary, and must have, therefore been developed as an independent centre of aggregation, of been abstracted from some other system. It should follow then, that, all the planets (which are satellites to the sun, just as truly as our moon is ours), having periods of rotation which differ radically with their orbital periods, must have formed as independent centres of aggregation, and cannot have been thrown off by the sun, as is sometimes maintained.

 

After the formation of our sun and the several members of our system with their orbital and diurnal motions as pointed out, there has been a constant tendency, developed by the contractions of the several masses, which is effective, even at the present time, in increasing the diurnal motions. In the first place, when the masses were in a gaseous condition, this contraction was large in amount in comparison to what is taking place in the present, so that it is not impossible to imagine that this increase in rotation, so correspondingly increased the contrifugal-force that first it equalled.

 

then exceeded the values of gravity at the surface of the several planets. In this last case, a result must have been the liberating of portions of their surface and their distribution in orbits about their equators, and if the increase in the diurnal-motion still continued, possibly the freeing of a continuous strip from off the equatorial regions, where this motion would have its greatest effect. In the first case we should have accounted for the formation of satellites, in the latter for “rings” such as we see about Saturn.

 

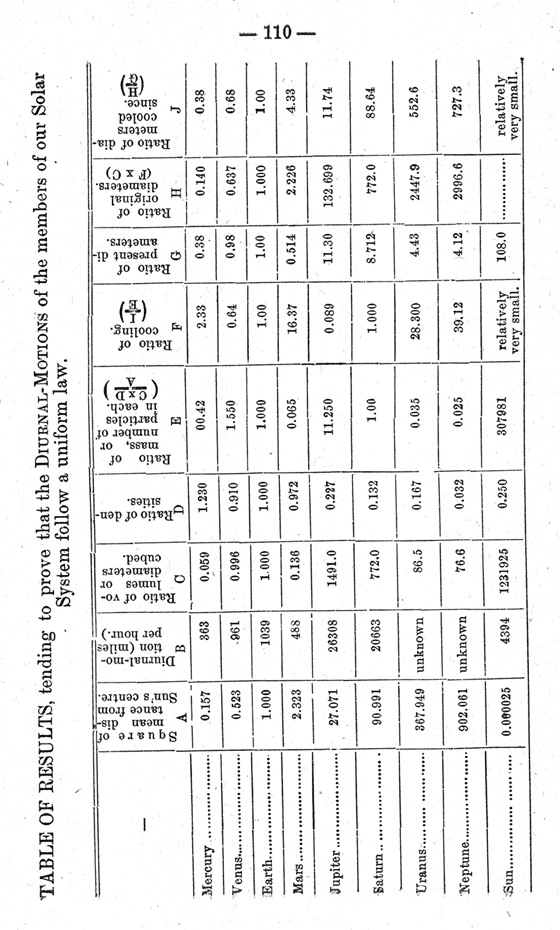
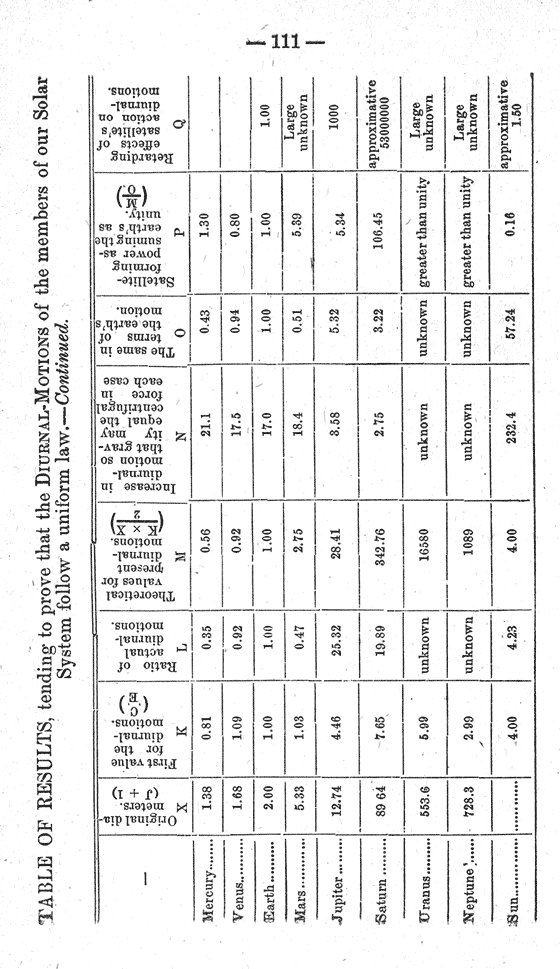
There are many points of interest, in the consideration of the general possibility of the contraction of a planet's diameters being sufficient to enable it to throw off its satellites, which the limited time at my disposal will prevent entering into. So that I shall start with the assumption that the diameters of all the planets have contracted owing to radiation, and endeavor to explain the contents of the accompanying “table”, which is intended to shew this effect in the individual cases of the members of our system.

 

It occurred to me, as it must have to most of us who have approached this subject, that if the planets of our system were developed by laws acting uniformly on the whole mass and each planet after formation, that all the motions common to each, should follow some general law, however intricate or at present disguised. Kepler found that the times in which each planet describes its orbit about the sun, followed a general law depending on their distance from that body. Newton found that the laws that had been known for centuries previously, as applicable to the effects of gravity at the surface of the earth, had a much more extended application, and governed the motions of all bodies no matter what their distance from the earth ; in other words, he proved from a particular application, the general truth of these laws, and how they controlled all matter in the universe. So, in the same way, it may be possible to identify the workings of common forces in the present diurnal-motions of the members of our system ; and, I may be excused for any shortcomings in my attempt to solve so extensive a question, when I assure you that, having attempted the investigation for my own information the satisfactory agreement in the results obtained, has tempted me to give them a more extended field, so that criticism, if you or others so will, may shew me in what particulars the reasoning employed has been faulty.

 

I do not propose treating this part of my subject in the same elementary way that I have done in the first case, as the time will not permit of it, but I shall give such explanations, as will make the arguments contained at the head of each column of the “table” amply sufficient for its full understanding.

 

As the diurnal-motions are the result of the difference in motion of the particles aggregated, as already explained, centres aggregating particles from equal areas, irrespective of the situation of these centres from the centre of the mass, will obtain equal diurnal motions ; and a very simple extension of this principle will shew, that if the limits of aggregation were twice as great, the diurnal-motion would be twice that of the first case, and so for any other limits we may set for this aggregation. At present we know what the volume of the several planets are, and very nearly, their densities ; and on the assumption, that having been produced from out the same original mass, they are each made up of the same material, we can determine the relative number of particles in each ; and assuming that these particles were comparatively evenly distributed about the original mass, (if this should not have been the approximate arrangement, they who are familiar with the operations which are to follow will know that complete discordance must result, and that the opposite being the case, the assumption is fairly upheld), their densities varied inversely as their distance from the centres of the mass, we can determine the relative areas over which each planetary centre aggregated its particles from ; hence, the amount of their initial diurnal-motions.

 

Then the number of particles that each centre contains, assuming all to have existed as parts of the original mass at nearly the same temperature, will give us the means of determining the rate at which these several centres radiated their heat, for this will have been directly proportionate to the mass, or number of particles in each ; and, assuming the cooling of a particular planet as being equal to unity, by means of this proportion, determine what this amount must have been in particular instances, and consequently, what increase in their diurnal-motions has resulted, and what, therefore, these motions should be to-day. This is the line of argument that I have followed, and it seems to me to be consequetive and substantial ; to those of you who may not be able or willing to follow me, I submit the fact, that this line of argument produces wonderfully close agreement in the results, or where there is disagreement, it is in a direction which is evidently so from the uncertainty that exists, either in the present accepted values of the diurnal-motion itself, in the quantities that have to be used in obtaining this theoretical value or can be accounted for from the fact of no allowance having been made for the disturbing influences of the satellites on their primaries, for it is in these cases only that this discrepancy exists, and that always in the direction required by these disturbing influences. And I submit to your investigation, any other line of reasoning that will result in such agreement, that you may either deduce for yourselves, or adopt at haphazard ; or follow the reasoning I have laid down, slightly altering any one of the steps, and decide for yourselves, whether the agreements that are obtained (six perfect ; one doubtful, and. two unknown, out of a total of nine instances), are not in themselves, some proof of the accuracy or the truth in the formulæ made us of.

 

The first four columns of my “table”, are quantities which are directly obtained from any text-book, so also are the columns “L” and “G” : the following explanations will make the remainder easily intelligible :—

 

“E “, would be simply CxD, were the particles of the original mass not arranged in the order of the densities of the particles, in which the heaviest are assumed to be nearest the centre of the mass, and the lightest furthest from it, varying, as our atmosphere does, inversely as the distance from the centre ; so that although two planets having the same mass or weight, have been developed at different distances from the centre of the mass, they must have a very different number of particles contained within them ; so that this column “E” is deduced by the continued product of C, x D, divided by A, or CxD/A.

 

Column “F”, the ratio of cooling (or the relative amount of heat radiated by any of the planets, in any assumed time), depending on the number of particles that each contains, irrespective of what may or may not have been the temperature of these particles at the time of aggregation, will be represented by the reciprocal of the quantities contained in column “E”, or be 1/E

 

Column “H”, the ratio that the original diameters of the planets bore to each other, would be equal to the cube of their present diameters, had no radiation and consequent cooling, taken place ; there having been a certain proportionate cooling, “C”, the ratio of the original diameters, is multiplied by “F”, the ratio of cooling. I may as well admit here, for you will be sure to find it out for yourselves, that this ratio of cooling, is a weak point in my arguments, not because it is impossible to imagine it as fulfilling the conditions required, but because it is impossible to demonstrate its truth ; for you will understand, that we are discussing a first condition of matter with which we have no experience, both because matter then existed at temperatures and in a condition of tenuity from which the conditions of the present allow of no experimental deductions. We can see for example, that a column of mercury loses appreciably a constant proportion of its volume for equal decrements of heat given out, and we are satisfied that although this may be very nearly the law up to the point where a change of its condition will take place; either on being vaporized or on freezing, yet we know that in either of these two altered conditions the law will necessarily require a change ; and, although we may be able to follow this change short distances in the required directions, we are not capable of asserting that any such law established will hold good for temperatures extremely beyond. Then, although we might not be far astray in the conclusions we might adopt in the case of a particular element, it is quite certain that we can form no estimate of the values to be given to the co-efficients of expansion or contraction where many elements are in combination, as in the case of the first conditions of our incipient planets. We should be quite certain however, that a planet does not lose equal units of its diameters for constant decrements of heat, but that the decrease in volume must have been a constantly diminishing quantity, such that the contractions in its first condition as a gaseous mass, were greater than when in its liquid or solid condition ; we must therefore adopt some such law as will contain this requirement ; and although we may not have determined the exact ratio of decrease, we shall certainly be somewhere near the true law ; how near, the amount of agreement in our results, will give us a fair means of determining. The ratio of cooling that I have adopted, assumes that the planatary bodies have lost for constant decrements of heat equal portions of the diameters then existing, so that if a planet in the first place lost one unit by contraction, it would lose at any later stage the same proportion of this unit that the then diameters were of the original diameters.

 

The remaining columns of my “table” contain sufficiently full information at their head, to enable any one to follow the reasoning made use of without further explanation, so that I will merely draw your attention to one or two of the conclusions, which I think are of importance, and which may escape your attention.

 

First, in the column “F”, we have the ratios of cooling, which at the same time represent how far the existence of each planet has progressed towards the final stage, of which our moon might be cited as an example. It will be seen that as far as conditions of existence are concerned, neglecting outside influences, the sun and Jupiter are the least advanced ; whilst Venus, although approaching the condition of the earth, on account of her nearness to the sun and the consequent alteration in this direction that must necessarily follow from his influences, should in reality be less advanced than the condition expressed. Mercury, although much further advanced than the earth, must have had this condition so altered by its proximity to the sun that its condition need not differ to any extent from that of the earth ; and indeed, the excess of the theoretical diurnal-motion over the observed value for the same, points to the same conclusion. Saturn exists to-day at a corresponding stage in its period of existence with the earth ; Uranus and Neptune, have passed much beyond our condition, and may be supposed to have very nearly reached the final and practically unaltering condition of an extinct world.

 

The column “P” containing the theoretical probability of each of the planets having satellite-forming powers, is worthy of passing notice. The earth being assumed as having formed a satellite by the centrifugal force exceeding-gravity, as the consequence of the contractions of her diameters, the same formulae are employed in every case, with the results seen in this column ; and I take it to be one of the most important pieces of evidence in favor of the truth of the arguments employed throughout, that in no case is there a theoretical satellite-forming power attributed to members, which do not shew the evidence of this power having been exercised in the possession of satellites to-day ; excepting in the case of Mercury, whose close proximity to the sun, has maintained an enormous retarding tidal-influence, which must have prevented the full development of the theoretical diurnal-motion, as already pointed out. Further, it will be noticed that the theoretical values deduced for this satellite-forming power, are approximately proportional to the existing number of satellites that each planet has ;—the larger the satellite-forming power theoretically, the greater the number of satellites ; and, in the case of Saturn, with the extreme power of 106, we find not only satellites in profusion, but rings. I have not explained why, if certain planets have so increased their rates of rotation, as to be capable of thus throwing off satellites, the motion could have been so reduced that the final outcome is a diurnal-motion much less than that necessary to do so, as it will have been evident to those at all conversant with the subject, that this liberation of satellites so acts that, immediately, the velocity of the remainder of the mass is reduced so that it is less than the required one ; and then, the newly formed satellites themselves, occupying their new orbits with linear velocities corresponding to that which they had at the surface of the planet, have a motion which is retrograde in comparison to the motion of a point at that surface ; and consequently act as a retarding influence upon the planet, so reducing its motion that similar developments become no longer possible.

 

In the case of the sun, several of the factors have to be ignored in arriving at our results, because of their insignificance proportionately to the values set for the same quantities in our planet of reference the earth ; so that column “F”, the ratio of cooling, being inversely as the number of particles in each member, becomes a relatively small quantity, in comparison to the value of unity we have set for our reference-body, the earth ; it has therefore to be left aside. So, for the same reasons, have the quantities belonging to the columns “H”, “J”, and “X” to be neglected. The quantity contained in column “K” then becomes the first value of the diurnal-motion, and is transferred to column “M”, directly, as the theoretical value of the present diurnal-motion ; knowing, that in so doing, we have ignored the acceleration, small as it should have been, that is attributable to the contraction of its diameters. Nevertheless, we have perfect agreement, remembering the omission, between the theoretical and visible diurnal-motions in this case, of 4.00 and 4.23.

 

Uranus and Neptune, the outlying sentinels of our system, being situated so far beyond us that the present means at the hands of the investigator, are insufficiently near to determine many of the factors that enter into my discussion ; most of the results, therefore, that have been deduced for the other members have been impossible to arrive at in their cases ; it is, however, possible to set extreme values for these, and by means of the same, say with some certainty, that in both cases the theoretical value for the diurnal-motion must have so increased, that satellites, possibly in the case of Neptune even a “ring”, may have been developed ; but that in any case, there should have been power sufficient to have produced several satellites, in each instance.

 

I feel that some apology is due, for having advanced the claim of discovery, in so well trodden a path, as that which surrounds the Nebular Hypothesis ; it may be unlikely that there is any additional information to be got out of a subject which has been so ably canvassed by other minds, but it should not be impossible. In any case, let me hope that if I have not convinced you of the value of my conclusions in this particular, that they have merited to some extent, the attention which you have so patiently given me this evening.