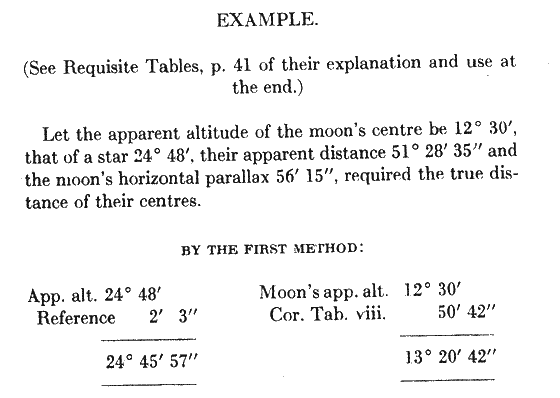
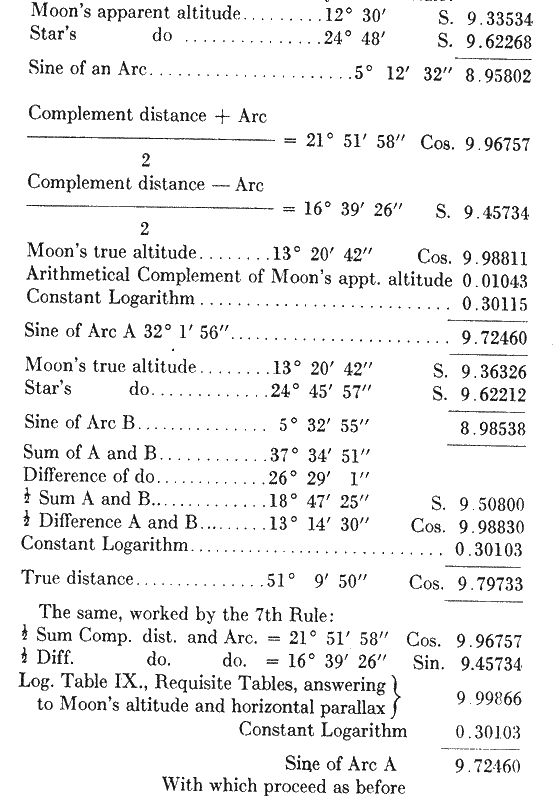
On the Different modes of reducing the apparent distances between the moon and the sun, or a star, in lunar observations, to the true distance for the purpose of ascertaining the longitude

 

by John Fletcher

 

[Originally published by the Literary and Historical Society of Quebec in Transactions, Original Series 3, Vol. 4, Number 1 (1837)]

 

(Presented to the Society, 18th March, 1837.)

 

Having been engaged some years ago in observations of this kind, I was induced to make some attempts to shorten this process, to which I was naturally led by the very considerable prolixity of all the methods described in the Requisite Tables.

 

My mode of considering the matter was as follows: —Let H 0, in the marginal figure, represent an arc of the horizon, Z the zenith, M H the moon's apparent altitude, her true or corrected altitude, S 0 the star's apparent altitude, and s 0 its corrected altitude. Now, it is obvious, that as the azimuthal angle, between the objects MZS, remains unchanged by the correction of    \their altitudes, the apparent distance M. S. becomes changed by the corrections into m s, which is the true or corrected distance to be discovered.

 

Our data for this are as follows: We have, firstly, in the triangle, M Z S, three sides, consisting of the apparent distance and the two apparent zenith distances given, to find the azimuthal angle at Z, and, having found, we have, also, in the triangle, m Z s, the two sides, m Z and s Z, (being the corrected zenith distances) and included angle at Z, to find the base m s, which is the true distance required. The direct mode therefore, of obtaining the true distance, is, of course, by the successive solution of the two triangles, M Z S and m Z s, and as this will not be found much more laborious than any of the methods described in the Requisite Tables, it is what I used generally to employ in preference to them, before I had the good fortune to hit upon shorter methods. To abridge and facilitate this solution, is, therefore, the object, both of myself and those who have devised the different modes of so doing (or rather, which are intended for that purpose) described in the Requisite Tables. Some of my methods are as follows: —

 

I.

 

1. Add together the two apparent altitudes and the apparent distance and take half their sum.

 

2. Take the difference between this half sum and each apparent altitude respectively.

 

3. Add together, the log. cosine of the moon's true altitude, the arithmetical complement of that of her apparent altitude, the log. sines of the before mentioned differences and the constant log., 0.30114, where the sun is taken, and 0.30115 where a star is taken, subtracting 30 from the Index and find the correspondent natural number.

 

4. Take the difference between the natural number and the natural cosine (to radius 1) of the difference of the true altitudes, and this difference will be the natural cosine of the true

distance, which will b3 less than 90°, if the beforementioned natural number is less than the last-mentioned cosine, and exceed 90° if it be greater.

 

                                                                           II.

 

1. Substitute, for the first two logarithms, mentioned in the last rule, (viz. the log. cosine of the moon's true altitude, and the arithmetical complement of that of her apparent altitude) the log., in tab. ix., in the Requisite Tables, answering to the moon's altitude and horizontal parallax, and substitute, also, for the constant logarithm, 0.30114 or 0.30115, the constant log. 0.30103, and proceed, in all other respects, as directed in Rule I.

 

* ** The above mentioned logarithm, from tab. ix., will be found sufficiently correct, in most cases being perfectly so, where the distance is taken from a star whose altitude is not less than 26°, and within 2 in the fifth place of decimals in every other assignable case. Where, however, mathematical accuracy is required, and the distance is taken from the sun, or a star under 26° high, the log., taken from table ix., may be diminished by the number answering to the sun or star's altitude in tables x. or xi. of the Requisite Tables.

 

III.

 

1. Add together, the log. cosine of the moon's true altitude, the arithmetical complement of that of her apparent altitude, and the log. sines of the differences between the apparent altitude of each luminary and the half sum of the true and apparent distance (as directed in the First Rule, articles I, 2, and 3,) and the constant log. 10.00012.[1]

 

2. From half the sum, subtract the log. sine of half the difference of the true altitudes, and the remainder is the log. tangent of an arc.

3. Subtract the log. sine of this arc from the beforementioned half sum, and the remainder is the log. sine of half the true distance required.

 

                                                                         IV.

 

1. Take the sum or difference of the natural cosine of the difference between the apparent altitudes and the natural cosine of the apparent distance, accordingly as the latter is greater or less than 90°
.

2. To the log. of this sum or difference add the log. cosine of the apparent altitude of the moon, the arithmetical complement of that of her apparent altitude, and the constant logarithm 0.00012, reject 10 from the index, and find the corresponding natural number.

3. The difference between this natural number and the natural cosine of the difference of the altitude is the natural cosine of the true distance, which is greater or less than 90° accordingly as this natural number is greater or less than the cosine of the difference of the true altitudes.

 

                                                                         V.

 

1. Take the sum or difference of the natural cosine of the. difference between the apparent altitudes, and the natural cosine of the apparent distance, accordingly as the latteris greater or less than 90°, as directed in the first precept of the last Rule.

2. To the common log. of this sum, or difference, add the log. from table ix., in the Requisite Tables, answering to the moon's altitude and horizontal parallax (corrected as stated in the note on Rule II., if thought necessary) subtract 10 from the Index and find the corresponding natural number.

3. The difference between this number and the natural cosine of the difference of the true altitudes is the natural cosine of the true distance, which will be greater or less than 90°, accordingly as this natural number is greater or less than the cosine of the difference of the true altitudes. I shall now proceed to work an example by each of these methods.

 

 

Which resulting log. being the same as that found above by the first method, and to be proceeded with in the same manner, will, of course, give the same result.

 

Which last log .being the same as that obtained by the First and Second Methods, and to be proceeded with in the same way, will, of course, give the same result.

 

BY THE FIFTH METHOD:

 

Diff. of nat. cosines of diff. app. alts.

and apparent distance found as                   35421  = 1.54925

log. the last Rule. .

           

answering to Moon's altitude and                    

Hor. parallax.                                                            1.54790

 

 

Which last log. being the same as that found above, by the 1st, 2nd, and 4th methods, and to be applied in the same way, will, of course, also, give the same result.

 

It will be perceived, that the preceding methods possess very considerable advantages. They are all capable of being made use of without the assistance of any other than common tables. Those, even consisting of only five decimal places, will, generally, if the proportional parts have been carefully taken, give the results true to the nearest second, and, always within 2" or 3", and, where those of six places are used, the error will never amount to 1".

 

P. S. Since writing the above, I find the following methods also amongst some of my papers, which, as they give the true distance in a different way, by finding its log. cosine, I have thought it worth while to insert, although they are somewhat longer than some of the preceding ones.

 

VI.

 

1. Add together the log. sines of the apparent altitudes, and the sum, rejecting 10 in the Index, is the log. sine of an arc

2. Take the half sum and half difference of this arc and the complement of the apparent distance (see example at end).

3. Add together, the log. cosine of this half sum, the log. sine of this half difference, the log. cosine of moon's true altitude, the arithmetical complement of that of her apparent altitude, and the constant log., 0.30114, where the distance has been taken from the sun, and, 0.30115, where the distance was taken from a star, and the sum, rejecting 20 in the Index, is the log. sine .of an arc, which call A.

4. Add together, the log. sines of the true altitudes, and the sum, subtracting 10 from the Index, is the log. sine of another arc, which call B.

5. Add together, the log. sine of the half sum, and the log. cosine of the half difference of the arcs of A and B, and the constant log., 0.30103, and their sum, rejecting 10 from the Index, will be the log. cosine of the true distance.

 

VII.

 

Substitute, for the log. cosine of the moon's true altitude and the arithmetical complement of that of her apparent altitude, mentioned in the third article of the last Rule, the log. in table ix. of the Requisite Tables, answering to the moon's altitude and horizontal parallax (corrected, as mentioned in Rule II., if thought necessary) and substitute ,also, for the constant log. 0.30114 or 0.30115, the constant log., 0.30103, and proceed, in all respects, as in the last Rule.

 

VIII.

 

1. The half sum of the logs, mentioned in Rule III., Art. 1, rejecting 10 from the Index; or, the half sum of the resulting log., obtained by either of the Rules, I., IV., or V., and the constant log., 19.69897, is the log. sine of an arc, to be taken out of the tables. Or, the half sum of the first three logs,, mentioned in Rule II., rejecting 5 from the Index.

2. The half sum of the log cosines of the sum and difference of this arc, and the half difference of the true altitudes, is the log. cosine of half the true distance.

 

*** The methods comprised in this last Rule are all variations of that which is called "Dunthorne's Improved," in the Requisite Tables, and are therefore, only inserted here to illustrate their analogy with the other methods, and the relation of these to each other.

 

                                            Modes of reducing Distances,.

 

  The preceding example worked by the 6th Rule: